Обновлено: 20.12.2023 14:57

Почему нельзя выиграть в рулетку

Item: Почему нельзя выиграть в рулетку
Rating: 4
Author: Vladislav Dibrov

Почему нельзя выиграть в онлайн рулетку в интернет казино? В этой статье мы приведем математическое обоснование отрицательного математического ожидания на дистанции при игре в азартную рулетку. Математическое доказательство неэффективности использования выигрышных стратегий в рулетке. Итак, почему нельзя выиграть в рулетку?

Почему нельзя выиграть в рулетку используя стратегии?

В качестве математического доказательства невозможности выиграть в рулетку рассмотрим все возможные простые ставки в рулетку и определим их МО (Математическое ожидание) результата.

В общем случае МО любой ставки в рулетке может быть рассчитано по классической по формуле (1):

, (1)

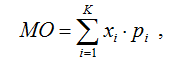
Где x_i– событие i,

р_i– вероятность события i,

К – общее количество событий, образующих полную группу.

Математическое ожидание Европейской версии:

Формула (1) для МО любой ставки на «Европейской рулетке» может быть преобразована с учетом полной вероятности не совместных событий, т.е. p_win_.+p_loss_.=1, к виду с учетом игры на N секторов (номеров), равна:

. (2)

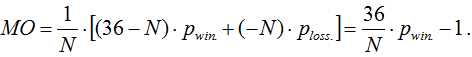
Так как вероятность выиграть р_win_.в «Европейскую рулетку» при игре на N секторов (номеров), равна:

, то окончательно получим выражение для МО для ЛЮБОЙ ставки в «Европейскую рулетку» при игре на N секторов (номеров), равно:

. (3)

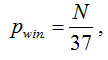
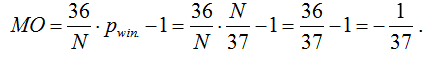
Сделаем расчет МО для каждой «простой» (элементарной) ставки в «Европейскую рулетку» (колесо с одним «Зеро»). Результат расчета МО для «простых» элементарных ставок представлен в 1 таблице.

Математическое ожидание для ставок:

Таблица 1. Расчет МО для «простых» ставок.

№	«Простая» Ставка	Выигрыш		Проигрыш	Расчет МО, у.е.
№	«Простая» Ставка	Выплата	Вероятность	Вероятность	Расчет МО, у.е.
1.	Straight-Up	35:1	1/37	36/37	=35×1/37-36/37= -1/37
2.	Split	17:1	2/37	35/37	=17×2/37-35/37= -1/37
3.	Street	11:1	3/37	34/37	=11×3/37-34/37= -1/37
4.	Corner	8:1	4/37	33/37	=8×4/37-33/37= -1/37
5.	Six Line	5:1	6/37	31/37	=5×6/37-31/37= -1/37
6.	Column & Dozens	2:1	12/37	25/37	=2×12/37-25/37= -1/37
7.	Even Chance	1:1	18/37	19/37	=1×18/37-19/37= -1/37

Как видно из таблицы – МО в точности равно значению, полученному по формуле (3). Подведем некоторые итоги.

Игрок проигрывает всегда, даже когда выигрывает

Играя в «Европейскую рулетку», игрок каждый спин, не зависимо от того, куда и сколько ставит, ВСЕГДА проигрывает 1/37 часть ставки (ставок). При этом МО игры не зависит от текущего результата спина, т.е. игрок проигрывает даже когда выигрывает. Или, другими словами, игрок проигрывает ВСЕГДА, когда делает ставку в «Европейскую Рулетку», не зависимо от результата текущего спина.

Использование стратегий ставок:

Для математического доказательства невозможности выиграть в «Европейскую рулетку» или «Американскую рулетку» достаточно ЛЮБУЮ СТАВОЧНУЮ стратегию разложить на «элементарные» ставки. Так как МО результата ВСЕХ ставок отрицательно и равно -1/37 от величины ставки, то и суммарное математическое ожидание результата игры будет отрицательно и равно -1/37 от суммы всех сделанных ставок игроком или -1/37 от величины средней ставки, умноженной на количество сыгранных спинов игроком.

Для оценки МО любой стратегии достаточно определить величину средней ставки при игре по данной стратегии, с учетом всех правил перехода от ставке к ставке, и умножить полученный результат на -1/37. Величины средней ставки и суммы всех сделанных ставок являются величинами положительными, следовательно МО всегда меньше нуля, т.е. МО£0 и меньше МО£–1/37, если используется прогрессия, т.к. величина средней ставки больше 1.

Дисперсия:

Рассчитаем дисперсию для ЛЮБОЙ ставки в «Европейскую рулетку» в зависимости от того, на сколько секторов N (номеров) ставит игрок. Дисперсию используем для определения оптимального банка по критерию Келли для игры в «Европейскую рулетку».

Справка:

банк по критерию Келли показывает, какой должен быть банк игрока, чтобы суммарный баланс всех игр стремился в бесконечность.

В общем случае Дисперсию игрока, играющего «Европейскую рулетку» на N секторов (номеров), можно рассчитать по выражению:

. (4)

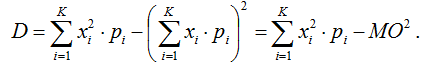
Формула (4) для дисперсии D любой ставки на «Европейской рулетке» может быть преобразована с учетом полной вероятности не совместных событий, , т.е. p_win_.+p_loss_.=1, к виду:

. (5)

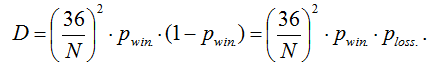
Так как вероятность выиграть р_win_.в «Европейскую рулетку» при игре на N секторов (номеров) равна:

, то окончательно получим выражение для дисперсии D при любой ставке в «Европейскую рулетку» при игре на N секторов (номеров), равно:

. (6)

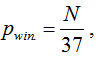
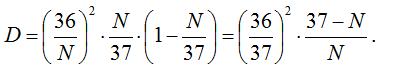
Величина дисперсии D – есть величина положительная во всем диапазоне игр на N секторов. Это очень важная деталь.

Откуда можно рассчитать требуемый банк для игры в «Европейскую рулетку», используя критерий Келли:

. (7)

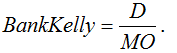
Используя выражения (3) и (6), окончательно получим выражение:

Математическое обоснование игры в рулетку

(8).

Из формулы (8) видно, что величина оптимального Банка по критерию Келли для игры в «Европейскую рулетку», является величиной отрицательной.

Вывод:

Если величина оптимального Банка игрока по критерию Келли является величиной отрицательной, то играть в «Европейскую рулетку» вообще не надо, так как суммарный результат баланса всех игр игрока стремится к нулю, или игрок при длительной игре должен проиграть все свои деньги.

Для оценки «привлекательности» азартных игр можно воспользоваться обобщенным критерием, который получен как отношение требуемого банка игрока по критерию Келли к математическому ожиданию результата игры, т.е.:

(9)

Из выражения (9) следует, что чем меньше величина требуемого банка игрока при данном математическом ожидании, тем «оптимальнее» игра для игрока. Данный критерий оптимальности можно трактовать, как критерий минимальности удельного банка игрока на единицу прибыли от игры.

Критерий оптимальности игры К_optimaможно использовать только для оценки игр с положительным математическим ожиданием! Для игр с отрицательным МО игра не может быть «привлекательной». Для «Европейской рулетки» МО равно –1/37, т.е. меньше нуля, поэтому «Европейская рулетка» как игра не «привлекательна» для игроков. Именно поэтому нельзя выиграть в рулетку, независимо от того, какие стратегии ставок и тактику выбора позиций вы используете.

Примечание: формулы (3), (5) и (8) могут быть получены и для «Американской рулетки» с двумя секторами Зеро: 0 и 00.

Где играть:

Выбирайте Fastpay казино и Betchan для крупной игры в рулетку. Эти операторы выводят деньги за несколько минут.
Попробуйте выиграть в рулетку не рискуя собственными деньгами. Получите бесплатно: 15$ в Riobet, 20$ в Play Fortuna.