Обновлено: 20.12.2023 10:23

Теория вероятности в онлайн-казино

Казино – продукт работы математиков, причем гениальных. Практически вся математическая база функционирования игорных заведений появилась еще очень давно и актуальна по сей день. Все знают, что заведение всегда остается в «плюсе». Но почему? Вроде бы вчера вы выиграли и вывели деньги. Как казино может получать прибыль? На самом деле все уже давно просчитано и основано на обычной теории вероятности – как, впрочем, и работа ваших любимых игр: будь то слоты, рулетка или покер. Теория вероятности изучает закономерности случайных явлений. Так написано в великой и могучей Википедии. Но что это означает в сфере азартных игр?

Исходы всех азартных игр, включая онлайн-слоты, случайны. Т.е. их нельзя предугадать заранее. Тут нам понадобятся математические законы теории вероятности, которые, на самом деле, довольно просты. Для начала же нужно понять, что любой спин в игровом автомате подчиняется определенным законам. Да, мы не знаем, каков будет результат отдельного вращения, но можем достаточно точно предугадать прибыль, к примеру, после 100 000 спинов. Теория вероятности в онлайн-казино состоит из множества теорем, законов и прочих устоявшихся знаний. Ключевыми для нас будут следующие понятия:

• математическое ожидание и случайная величина,
• дисперсия случайной величины,
• нормальное распределение,
• центральная предельная теорема,
• закон больших чисел,
• математическое ожидание бонусов казино
• и рекомендация, где играть надежно.

В принципе, нам больше ничего не нужно для описания работы всей казиношной машины. А это, на минуточку, сложный и огромный организм! В общем, давайте по порядку.

Математическое ожидание

В азартных играх важно примерно представлять свою потенциальную прибыль. Математическое ожидание как раз и помогает это сделать. Оно показывает среднее значение случайной величины.

Что такое случайная величина в тех же игровых автоматах? Это выигрыш отдельного спина! Таким образом, математическое ожидание показывает среднее значение нашего выигрыша.

И если вы хоть немного разбираетесь в работе современных слотов, то прекрасно знаете о существовании такого показателя как процент выплат (Return to Player). Он-то, по сути, и будет являться нашим матожиданием. Процент выплат показывает, сколько на длительном отрезке времени отдаст слот.

Например, 96%. Это означает, что автомат запрограммирован отдавать на дистанции (т.е. после огромного количества спинов) 96% от вложенных в него ставок. Не в каждом вращении, а после большого их количества. Эти же 96% можно назвать матожиданием конкретной игры. Только матожидание не выражается в процентах, оно может быть в пределах от -1 до 1. Так что наши 96% трансформируются в -0.04. И, следовательно, математическое ожидание отрицательно. На дистанции в среднем это будет означать 4% проигрыша.

• Как получить плюсовое математическое ожидание в казино?

Матожидание может быть и положительным, просто в случае с казино это происходит крайне редко. К примеру, такое может произойти в блэкджеке (при счете карт), но в интернет-заведениях с этим куда сложнее (потому что колода бесконечная). Или еще при игре с выгодным бонусом – допустим, 200% с вейджером х25.

Отрицательное математическое ожидание, т.е. потенциальная прибыль игрока – это абсолютно стандартно для почти что всех игр казино.

По сути, игрок не может получить прибыль на дистанции (но зато может выиграть много на краткосрочном отрезке), так что не стоит пытаться сделать свое хобби единственным источником заработка. Это скорее развлечение, за которое приходится платить.

• Узнайте больше о математике в казино.

Дисперсия случайной величины

Дисперсия – это мера отклонения случайной величины от математического ожидания. Грубо говоря, это мера отклонения от среднего значения.

Например, возьмем слот Space Wars. Он считается высокодисперсионным, что означает большое отклонение случайных величин от математического ожидания. На языке игроков это звучит так: «Жрет, как пылесос!». «Жрет» слот потому, что может выдавать крупные выигрыши. А как еще можно сбалансировать крупные выплаты, если не затяжными периодами сливов?

В Space Wars (условно) игрок может получить максимум х5 000 за спин. Но закон работает и в обратную сторону, следовательно, и пул максимальных проигрышей (т.е. череды пустых вращений) тоже удлиняется. В другом же игровом автомате максимальный выигрыш может равняться х1 000 за спин. Следовательно, он гораздо менее дисперсионный. Здесь есть один важный момент. Чем выше отклонения от математического ожидания, тем больше будет «нестандартных» исходов. Например:

• исход 1: выигрыш х100,
• исход 2: 10 пустых вращений,
• исход 3: выигрыш х10
• исход 4: выигрыш х2,
• исход 5: 20 пустых вращений,

и т.д. Даже после сотен спинов мы можем не приблизиться к среднему значению случайной величины – к математическому ожиданию. Тот же Space Wars отдает 96.8% на дистанции. Если хотите, можете примерно прикинуть, сходятся ли ваши результаты с этим значением. Хотя можете не утруждаться – скорее всего это не так. Вы можете быть в большом «плюсе» или крупном «минусе», но вряд ли сыграли в ноль даже после большого количества спинов. Почему? Потому что высокая дисперсия.

Нормальное распределение

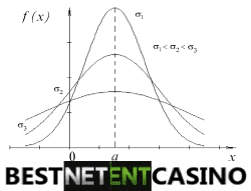
Нормальное распределение – распределение вероятностей, напрямую зависящее от значений математического ожидания и дисперсии. Вероятнее всего, вы уже не раз с ним сталкивались. Этот тот самый колоколо-образный график, самая высокая точка которого (пик) как раз и соответствует значению математического ожидания (средней величине).

Иными словами, нормальное распределение описывает спектр разброса случайных исходов. В нашем случае это будут вращения рулетки, спины в слотах или броски кубиков в крэпсе. Чем выше дисперсия, тем ниже будет максимальный пик графика. И наоборот: чем ниже дисперсия, тем выше максимальное значение.

В случае автомата Space Wars график его нормального распределения похож на небольшой холмик. Это объясняется большим разбросом всех исходов. К примеру:

• исход 1: выигрыш х50 (ставим точку на графике правее),
• исход 2: 10 пустых вращений (рисуем точки левее),
• исход 3: выигрыш х200 (точка еще правее),
• исход 4: выигрыш х2 (точки практически посередине графика),
• исход 5: выигрыш х2 000 (точка почти на самом краю справа).

и так далее. Из всех исходов (точек) и складывается график. Большинство вращений дают незначительные выигрыши и проигрыши и потому сосредоточены у центра. Но все крупные выигрыши и многочисленные периоды постоянных сливов «сплющат» график, как бы растянут его в стороны. Нормальному распределению подчиняются все случайные величины, если они образуют большой массив слабо зависимых между собой данных. И тут, кстати, можно упомянуть еще один важный математический закон.

• Узнайте больше об адаптивной математике

Центральная предельная теорема

Центральные предельные теоремы в целом утверждают следующее: если перед нами большая выборка практически не связанных друг с другом случайных величин и ни одна из них не является доминирующей, тогда их распределение будет стремиться к нормальному.

Центральных теорем несколько, но все они говорят примерно об одном и том же. В казино все это тоже применимо и отлично работает.

Закон больших чисел

Закон больших чисел – это, по сути, синоним предельных теорем. Он гласит: при достаточно большом количестве случайных, одинаково распределенных величин их среднее значение стремится к их математическому ожиданию. То же самое, только немного другими словами.

Как видите, ключевыми в казиношной теории вероятности являются понятия математического ожидания и дисперсии, а вокруг них формируются все аксиомы, теоремы и законы.

Закон больших чисел универсален и работает во многих областях, не только в казино. В обывательском смысле он демонстрирует возможность положительного исхода на крайне большом массиве случайных данных. Часто в качестве примера приводят вероятность появления жизни на Земле. Если вероятность ее возникновения 1 из миллиарда планет, а в условной галактике 30 миллиардов планет, значит, еще на 30 из них есть жизнь. Но это очень спорное применение данного закона.

Математическое ожидание бонусов казино

Довольно интересно и полезно вычислять матожидание конкретных бонусных предложений. Это довольно просто, для этого нам понадобятся следующие значения:

• вейджер,
• преимущество казино в игре для отыгрыша бонуса,
• величина бонуса.

Итак, сначала берем вейджер (допустим, он равен х50) и умножаем его на величину бонуса (например, $ 100), чтобы узнать общую сумму ставок. У нас получилось $ 5 000 (50 * 100 = 5 000). Т.е. нам нужно сделать ставок на сумму $ 5 000, чтобы отыграть выданный бонус 100% на первый депозит, вполне стандартные условия. Далее, умножаем $ 5 000 на преимущество заведения в конкретной игре. Скорее всего это будет какой-нибудь слот, в автоматах NetEnt отдача чаще всего составляет примерно 96%, значит, преимущество казино 4% : 5 000 * 0.04 = $ 200. Это мы получили теоретическое значения проигрыша после проставления $ 5 000 в виде ставок. Это очень приблизительно, чаще всего практическое значение сильно отличается.

Дальше из бонуса отнимаем теоретический проигрыш и получаем математическое ожидание: 100 – 200 = -$ 100. Выходит, бонус брать не выгодно.

Таким же способом можно посчитать «прибыльность» любого бонусного предложения. Но учтите, что это все теория, в большинстве случаев у вас будут совершенно иные результаты на практике.

Где играть

• Используйте знания о теории вероятности в Fastpay казино и Betchan. Эти операторы выводят деньги за несколько минут.
• Попробуйте разобраться с теорией вероятности в казино не рискуя собственными деньгами. Получите бесплатно: $ 15 в Riobet, $ 20 в Play Fortuna.

Возможно, вам так же будут интересны следующие разделы:

• Математика стратегии Мартингейла
• Математическое ожидание в казино Netent
• Как выиграть в казино с помощью математики?

Лучшие онлайн-казино для игры на деньги 2024