Last Updated: Monday, 06 January 2025 11:48
Why is it impossible to win at roulette?

Why cannot you succeed in roulette via using strategies?

In the general case, I of any bet in roulette can be calculated using the classical formula (1):
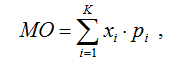
- Where is xi– event I,
- Pi– The probability of the event I,
- К – The total number of events forming a complete group.
The mathematical expectation of the European version:

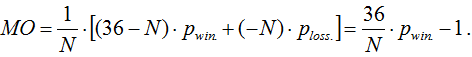
Since the probability of winning Pwin in "European roulette", while you are playing for N sectors (rooms), is equal to:
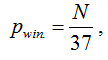
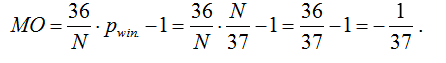
Let's calculate ME for each "simple" (basic) bet in "European roulette" (a wheel with one zero). The result of ME calculation for average basic bets is presented in table 1.
The mathematical expectation for the bets:
Table 1. Calculation of ME for "simple" bets.
№ | «Simple» bet | Winning | Loss | Calculation МО, у.е. | |
Payout | Probability | Probability | |||
1. | Straight-Up | 35:1 | 1/37 | 36/37 | =35×1/37-36/37= -1/37 |
2. | Split | 17:1 | 2/37 | 35/37 | =17×2/37-35/37= -1/37 |
3. | Street | 11:1 | 3/37 | 34/37 | =11×3/37-34/37= -1/37 |
4. | Corner | 8:1 | 4/37 | 33/37 | =8×4/37-33/37= -1/37 |
5. | Six Line | 5:1 | 6/37 | 31/37 | =5×6/37-31/37= -1/37 |
6. | Column & Dozens | 2:1 | 12/37 | 25/37 | =2×12/37-25/37= -1/37 |
7. | Even Chance | 1:1 | 18/37 | 19/37 | =1×18/37-19/37= -1/37 |
As can we see from the table – ME is exactly equal to the value obtained by the formula (3). Let's sum up the results.
The player always loses even when he wins

Using the strategies of the bets:
For the mathematical proof of the winning's impossibility at "European roulette" or "American Roulette," it is enough to expand any betting strategy on the "basic" bet. As ME result of all bets is negative and equals -1/37 the size of the stake, then the total expectation of the game result will be negative and equal -1/37. The sum of all bets made by the player or -1/37 from the value of the average stake multiplied by the number of spins played by a gambler.
Assessing the ME of any strategy is enough to determine the value of the average bet while you are playing according to this strategy and taking into consideration all the rules of the transition from bet to bet, and multiplying the result by -1/37. The value of the average bet and sum of all of the bets are positive values; therefore ME is always less than zero, that is ME£0 and less than ME£-1/37 if used the progression because the average rate is bigger than 1.
Dispersion
Let's calculate the variance for any bet in "European roulette", depending on how many sectors N (rooms) puts the gambler. Use the variance to determine the optimal Bank Kelly criterion for playing "European roulette".
Information
Bank on Kelly's criterion shows what should be the gambler's bank to the total balance of all games aspired to infinity.
In the general case, the variance of the player who is playing at the "European roulette" in N sectors (rooms) can be calculated by the expression:
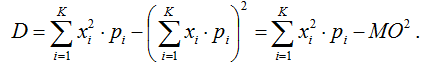
The formula (4) for the variance D of any bets on the "European roulette" can be converted taking into the full probability, not joint events, that is Pwin.+ Ploss.=1, to the mind:
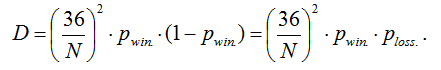
Since the probability of winning Pwin in the "European Roulette" while you are playing for N sectors (rooms) is equal to:
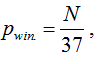
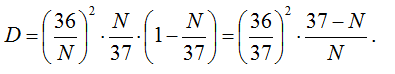
The magnitude of dispersion D has a positive value throughout the range of games in N sectors. That is an important detail.
Where it is possible to calculate the required bank for the game at "European roulette" using Kelly's criterion:
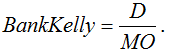
Using the expressions (3) and (6), we finally obtain the expression:

The formula (8) shows that the optimal amount of the bank, according to Kelly's criterion for playing at "European Roulette" is a negative value.
Conclusion:
If the optimal value of the gambler's bank following Kelly's criterion is negative, then playing at "European roulette" is generally not necessary, since the overall result of the balance of all players` games approach to zero, or the player has to lose all his money during the long game.
To assess the "attractiveness" of the gambling, you can use generalised criteria, which is obtained as the ratio of required the gambler's bank following Kelly's criterion to the mathematical expectation of the game result that is:

This expression (9) can be understood that the smaller size of the gambler's bank at the mathematical expectation, the "better" will be a game for the player. This optimal criterion can be interpreted as the criteria of minimal specific player's bank per unit of profit from the game.
The optimal criteria of the Кoptima game can only be used for evaluation of games with a positive expectation! If the game has a negative MT, it will not attract the attention of the gamblers. For "European roulette" MT -1/37, that is less than zero, so "European roulette" as the game is not "attractive" for gamblers. That is why it is impossible to win in roulette, regardless of which betting strategies and tactics selection of items you use.
Note: the formula (3), (5) and (8) can be obtained for "American roulette" with two sectors of zero: 0 and 00.
Similar materials
Where to play?
- Choosing an honest is an important step before you start playing in live games or slots. Our highly recommended is Fastpay casino. They will send the money within 5 minutes.





